2023학년도 수학 능력 시험 수학 과목 선택 영역인 확률과 통계 미적분, 키(23~30번까지 자세한 해설을 합니다.2023학년도 수능은 2022년에 시행한 수능입니다.2023수학 능력 시험 수학의 공통 이유로 한번부터 22번까지 해설은 따로 올렸습니다.필요한 분은 아래의 링크를 확인하십시오.수학 능력 시험 수학 1~10번까지 해설

2023 SAT수학 가장 빠른 해설과 수학 문제 정답 PDF파일 2023학년도 대학 수학 능력 시험 수학 문제 파일과 빠르며 파일, 그리고 1~10번까지 제가 직접 해설한…m.blog.naver.com

수능 수학 11번부터 22번까지의 해설

네트워크에 접속할 수 없습니다.
연결 상태 확인 후 다시 시도해주세요.

수능 수학 11번부터 22번까지의 해설
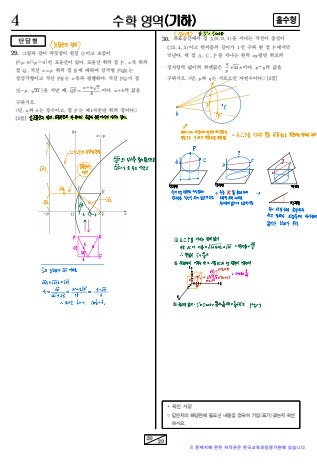
2023 수능 수학확대 23번 24번 해설2023 수능 수학확대 23번 24번 해설2023 수능 수학확대 23번 해설수학 능력 시험 수학 과목 확대 23번 문제는 매우 쉽죠?항상 나오는 타입이라서요, 틀리지 않도록 꼭 공식 외어 두세요.x의 9제곱이 되려면 x3제곱항을 3번 곱하면 되죠?2023 수능 수학확보 24번 해설수능수학확대24번문제는먼저4000이상으로하려면천자리수가4나5여야하죠? 그리고 홀수이기 위해서는 일의 자릿수가 1, 3, 5인 3개의 홀수가 와야 합니다. 그리고 중복을 허용한다는 것을 꼭 기억하세요.2023 수능 수학확보 25번 26번 해설2023 수능 수학확보 25번 26번 해설2023 수능 수학확대 25번 해설수학 능력 시험 수학 과목 확대 25번 문제는 여자 사건으로 해설했습니다.적어도 1개가 흰 마스크의 확률을 해서 1에서 모두 검은 확률을 뽑아 주었습니다.그리고 2개의 해석 방법으로 설명했는데, 사실 처음의 해석이 쉽고 가독성이 좋습니다.그러나 굳이 2번째 해설도 한 이유는 조합 공식을 이용하고 정석대로 푸는 방법도 알아 두면 좋을 것으로 해설했습니다.양쪽의 해법을 이해하고 두세요.2023 수능 수학확보 26번 해설수학 능력 시험 수학 과목 확대 26번을 해설합니다.A와 B의 합집합의 확률을 구하려면 A와 B의 각각의 확률을 가하고, A와 B의 교집합의 확률을 빼면 됩니다.전체의 경우는 6개의 볼에서 3개의 공을 꺼내게 되므로, 6C3이 됩니다.손 해설에서 매우 잘 썼으므로 텍스트의 더 이상의 설명은 생략합니다.2023 수능 수학확보 27번 28번 해설2023 수능 수학확보 27번 28번 해설2023 수능 수학확보 27번 해설수학 능력 시험 수학 과목 확대 27번 문제 해설입니다.95%의 때는 1.96으로 99%의 때는 2.58입니다.신뢰 구간을 위와 같이 구한 후, n의 범위를 요구할 수 있습니다.2023 수능 수학확보 28번 해설수학 능력 시험 수학 28번 문제 해설입니다.b이하 때는 8분의 5로 b이상 때는 8분의 3이라, 윗 그림과 같이 5:3이 됩니다.그러니까 a는 8k와 두고 b는 5k으로 둡니다.루트 5이하는 2분의 1로 8분의 5는 2분의 1보다 크고 b는 루트 5보다 큽니다.루트 5이하 때는 넓이가 2분의 1이므로 삼각형의 넓이를 이용하고 k의 값을 요구할 수 있습니다.그래서 구하고 싶은 답이 나오네요.2023 수능 수학확대 29번 30번 해설2023 수능 수학확대 29번 30번 해설2023 수능 수학확대 29번 해설확보 29번 문제는 분류해서 찾아보겠습니다.모든 수의 합이 짝수인 위해서는 홀수가 3회 나오느냐 홀수가 1번 나가면 됩니다.홀수가 3번 나올 때는 같은 수가 3번 나오는 경우 같은 수가 2회 나올 경우 3번 모두 다른 수로 나누고 경우의 수를 요구합니다.1이 한번만 나갈 때는 3개의 수가 모두 다른 때와 2개의 수는 같은 1이 나올 경우 2개의 수는 짝수인면서 1이 있을 경우에 나누어 경우의 수를 요구하면 됩니다.2023 수능 수학확보 30번 해설수학 능력 시험의 확대 30번의 해설입니다.조건 나에 의해서 f(1)=1, f(10)=10이 됩니다.조건 다에 의해서 f(5)=1때는 f(6)=7이 됩니다.f(5)이2때 3때 4때 경우를 나누어 각각의 값을 요구합니다.1번째는 4번째와 비슷한 상황에서 2번째는 3번째와 비슷한 상황에서 입수할 수 있습니다.2023학년도 수능 시험 수학 선택 영역 미적분 해설합니다.2023년 수능 수학 미적분 23번 24번 해설2023년 수능 수학 미적분 23번 24번 해설2023년 수능 수학 미적분 23번 해설수능 수학 미적분 23번 해설입니다. 분모에 루트가 있기 때문에 공역을 분모 분자에 곱합니다. 그리고 x의 값인 0을 대입하면 답이 나오네요.2023년 수능 수학 미적분 24번 해설미적분 24번 해설입니다. 핑크 하이라이트 부분 보이시죠? 따라서 1부터 4까지 적분하시면 됩니다.2023년 수능 수학 미적분 25번 26번 해설2023년 수능 수학 미적분 25번 26번 해설2023년 수능 수학 미적분 25번 해설수능 수학 25번 해설입니다. 문제에서 주어진 극한값이 3으로 존재하기 때문에 r은 4여야 합니다. 그리고 4의 n제곱 계수를 비교하면 a 값을 구할 수 있습니다. 따라서 등비수열의 두 번째 항의 값이 나오죠.2023년 수능 수학 미적분 26번 해설수학 능력 시험 수학 26번 문제 해설입니다.체적은 넓이를 적분하면 됩니다.정방형의 넓이는 한 변의 길이의 제곱입니다.그러므로 위와 같이 나옵니다.sec제곱을 적분하면 탄젠트가 되고, 탄젠트를 적분하면 lncosx입니다.모의 시험이나 수능 시험을 치르기 전에 삼각 함수의 미분과 적분치를 다시 한번 확인하세요.물론 평소 다 외우고 두지 않으면 안 되고, 수학 능력 시험 며칠 전, 모의 시험 며칠 전에 수학은 무엇을 공부해야 할지 모른다는 학생이 있습니다.이럴 때는 수학 공식집을 훑어보며 것도 추천입니다.공식만 알면 눈을 풀문제도 많은데, 공식을 혼란시키고 잘못하면 너무 억울하잖아요.2023년 수능 수학 미적분 27번 28번 해설2023년 수능 수학 미적분 27번 28번 해설2023년 수능 수학 미적분 27번 해설수학 능력 시험의 미적분 27번 문제 해설입니다.문제의 그림에 몇 차례 해설을 쓰자니 너무 복잡하게 보이는 것 따로 그리고 해석했습니다.별로 그린 그림과 문제의 그림을 비교하며 어느 부분의 것인지 확인하면서 해설을 보세요.이 타입의 문제는 제가 항상 말하고 있지만 문제는 길고 그림은 복잡하게 보이는 것에서 낮은 등급 학생은 읽지 않고 포기하는 경우가 많습니다.그러나 이 유형의 문제는 생각보다 정말 간단한 문제라서 포기하지 않고 꼭 풀어 보세요.첫번째 그림의 넓이와 공비만 요구하면 바로 답이 나올 문제입니다.최근 이 타입의 문제는 계속 사치비를 이용하는 문제로 나오고 있습니다.이 타입의 문제는 반드시 바로잡아야겠죠!^^2023년 수능 수학 미적분 27번 해설확실히 나는 선명한 상태에서 사진을 올리는데 왜 해상도가 떨어지고 오르는지 모르겠네요.이거 누군가 아는 분이 계시다면가르치세요 아무튼 사진을 클릭하면 좀 더 보기 좋을까요, 확대하면 해상도가 조금 떨어지는 듯한 것으로 해설 과정만 따로 스크랩 업했습니다.문제와 함께 스크랩한 것보다 선명하지 않느냐는 마음으로 올릴게요.2023년 수능 수학 미적분 28번 해설수능 수학 미적분 28번 문제 해설입니다. 이 문제는 복잡해 보이지만 계산이 깔끔하기 때문에 저는 이런 문제가 편하네요. 분수 계산 더러운 문제 싫어요 가독성을 위해 같은 색으로 강조 표시했어요. 참고해 보세요.2023년 수능 수학 미적분 28번 해설이번에도27번과똑같이확대했을때조금이라도선명도가좋아질까해서문제는빼고그림을따로풀어봤습니다. 조금 나은지 모르겠네요.2023년 수능 수학 미적분 28번 해설위 해법 과정의 사진을 클릭하여 확대하면 문제처럼 있는 해법보다 선명해지길 바랍니다.2023 수능 수학 미적분 29번 30번 해설2023 수능 수학 미적분 29번 30번 해설2023년 수능 수학 미적분 29번 해설수학 능력 시험 수학 미적분 29번의 해설입니다.우선 f함수의 a, b, c를 요구합니다.하면 완전한 f함수식으로 나타납니다.f함수의 역함수는 g함수이므로 g함수가 0때와 14때의 값을 f함수에 대입하고 요구합니다. x를 f(t)으로 한 후에 미분합니다.그리고 적분할 때 그적 미적 공식은 아시죠?이를 이용해서 적분하고 미리 찾아 둔 값을 대입하고 계산하시면 됩니다.그레이의 하이라이트 부분을 참고하세요.2023년 수능 수학 미적분 30번 해설수학 능력 시험 수학 미적분 30번의 해설입니다.사인 함수의 최소치는-1로 최대치는 1이라 g함수의 최소, 최대가 나타납니다.그래서 계략적인 그래프를 그릴 수 있습니다.조건 나를 통해서 f(x)=0에서 극치를 가졌음을 알 수 있습니다.f'(3)=0, f(3)=1/2로 f함수는 최고 차항의 계수가 양수인 삼차 방정식임을 알리고 준 것이 f함수의 대략적인 그래프를 그릴 수 있습니다.상기의 계산을 통해서 꼭대기에서 그린 g함수와 f함수에 대해서 더 자세히 알 수 있습니다.상기의 손 해설에서 자세히 해설하였으므로, 손 해설을 참고하세요.2023학년도 수능 시험 수학 선택 영역 기하 해설입니다.2023 수능 수학 기하23번24번 해설2023 수능 수학 기하23번24번 해설2023년 수능 기하 23번 해설수능 수학 기하 23번 해설입니다. x축에 대칭이면 y와 z의 부호가 반대로 바뀌겠죠? 그래서 B의 좌표는 (2,-2,1)이 됩니다. B와 C의 z 좌표는 서로 같기 때문에 선분 길이를 구할 때 x 좌표와 y 좌표 값만 계산해도 됩니다.2023년 수능 기하 24번 해설수학 능력 시험 수학의 키(24번 해설입니다.y2=4px에 p의 값 3분의 1을 대입합니다.그렇게 포물선식이 나오면(a, 2)을 대입하고 a의 값을 요구합니다.2023 수능 수학 기하25번 26번 해설2023 수능 수학 기하25번 26번 해설2023년 수능 기하 25번 해설수학 능력 시험 수학이 하 25번의 해설입니다.우선(2,1)을 대입합니다.그리고 x에 대해서 미분해서 3번식을 요구합니다.3번식에(2,1)과 접선의 기울기를 대입하고 a와 b의 관계식을 요구합니다.2번식과 4번식을 연립해서 a와 b의 값을 요구합니다.초점을 c로 할 때 공식에 대입하고 c의 값을 요구할 수 있습니다.c의 값이 루트 6이 나왔으니 2개의 초점 간의 거리는 2루트 6이 됩니다.2023년 수능 기하 26번 해설수능 수학 기하 26번 해설입니다.중심은 (2,6), 반지름은 2가 됩니다. 그리고 벡터 q는 y=2 위의 임의의 점입니다. 따라서 최소치가 될 때는 위 그림에서 표시한 부분일 때입니다. 따라서 최소치는 2가 됩니다.2023 수능 수학 기하 27번 28번 해설2023 수능 수학 기하 27번 28번 해설2023년 수능 기하 27번 해설수학 능력 시험 수학의 키(27번의 해설입니다.문제에서 사인 세 타원의 값을 일러줬기 때문에 첫 그림을 이용하고 코사잉세 타원의 값을 요구할 수 있습니다.그리고 2번째 그림으로 코사잉세 타원의 값을 이용하고 선분 CH2의 값을 요구할 수 있습니다.세 수선 정리에 의해서, 선분 AB과 선분 H1H2의 값이 수직으로 나타납니다.피타 고라스 정리에 의해서 선분 H1H2의 값이 요구됩니다.이로써 코사인 세타토우의 값이 얻을 수 있습니다.2023년 수능기하 28번 해설수학 능력 시험 수학이 하 28번의 해설입니다.쌍곡선의식과 점근선 공식을 통해서, b와 c를 a에 관련된 양식으로 표현할 수 있습니다.쌍곡선의 정의와 코사인의 법칙도 이용합니다.a은 0이 아니라서 a는 8분의 9로 주축은 2a이므로 4분의 9입니다.2023 수능 수학 기하 29번 30번 해설2023 수능 수학 기하 29번 30번 해설2023년 수능 기하 29번 해설수학 능력 시험 수학의 키(29번의 해설입니다.위의 손의 해석에 최대한 쉽게 그렸습니다.보라 색 부분은 문제로 제시한 것이거나 그들로 금방 알것입니다.그 다음 단계로 핑크의 부분을 참고하세요.벡터 CA와 벡터 DQ의 내적은 서로 수직인 것으로 0이 되니까 답은 12에 됩니다.2023년 수능 기하 30번 해설수학 능력 시험 수학 기하 30번 해설입니다.삼각형 BCD는 정삼각형으로 공의 반경은 6그래서 아폴로니우스의가 2대 1이라 나머지 길이가 3이 됩니다.그래서 높이는 6+3=9입니다.정삼각형의 높이 공식을 이용하고, 한 변의 길이가 6루트 3이 될 압니다.왼쪽 첫번째 그림을 통해서 코사인 시 타원의 값을 요구됩니다.2번째 그림에서 선분 PB는 4경로 3로 선분 AP의 길이는 2루트 3으로 나타납니다.정사면체 A-PQR의 한 변의 길이가 2루트 3이기 때문에 정삼각형의 PQR의 넓이는 정사각형의 넓이를 구하는 공식을 이용하여 요구됩니다.오른쪽 첫번째 그림에서 선분 PH3의 값을 요구할 수 있습니다.오른쪽 2번째 그림에서, 코사인 세타토우의 값으로 나타납니다.삼각형 PQR의 넓이와 평면 알파의 뿔은 세타 투로 정사영의 넓이는 정삼각형 PQR의 넓이 3루트 3 걸코사인 세타 투의 값을 대입하고 계산하시면 됩니다.이렇게 2023학년도 대학 수학 능력 시험 수학 과목의 전체 해설을 마치겠습니다.최초의 포스트는 2023년 수학 능력 시험 수학 공통 영역 1~10번까지 설명, 2번째는 11~22번까지 설명, 지금 이 자리는 수학 선택 영역의 확대, 미적분, 키(23~30번까지 해설입니다.2022수학 능력 시험의 해설이나 2021수학 능력 시험의 해설은 홈 화면에서 수능 카테고리에 있습니다.2022년 2021년 등 기타 많은 모의 시험 해설은 모의 시험 카테고리에 있으니 필요한 분은 참고하세요^^수학 능력 시험을 받은 수험생 여러분 수고 하셨습니다.성적표가 나오기 전까지는 그냥 푹 쉬고 열심히 놀것을 추천합니다.다음의 포스트에서는, 입시 정보나 교육 정보 자리에서 찾아뵙겠습니다.

